Posted on

Random Forests and The Power of Guessing for Low Incidence Features

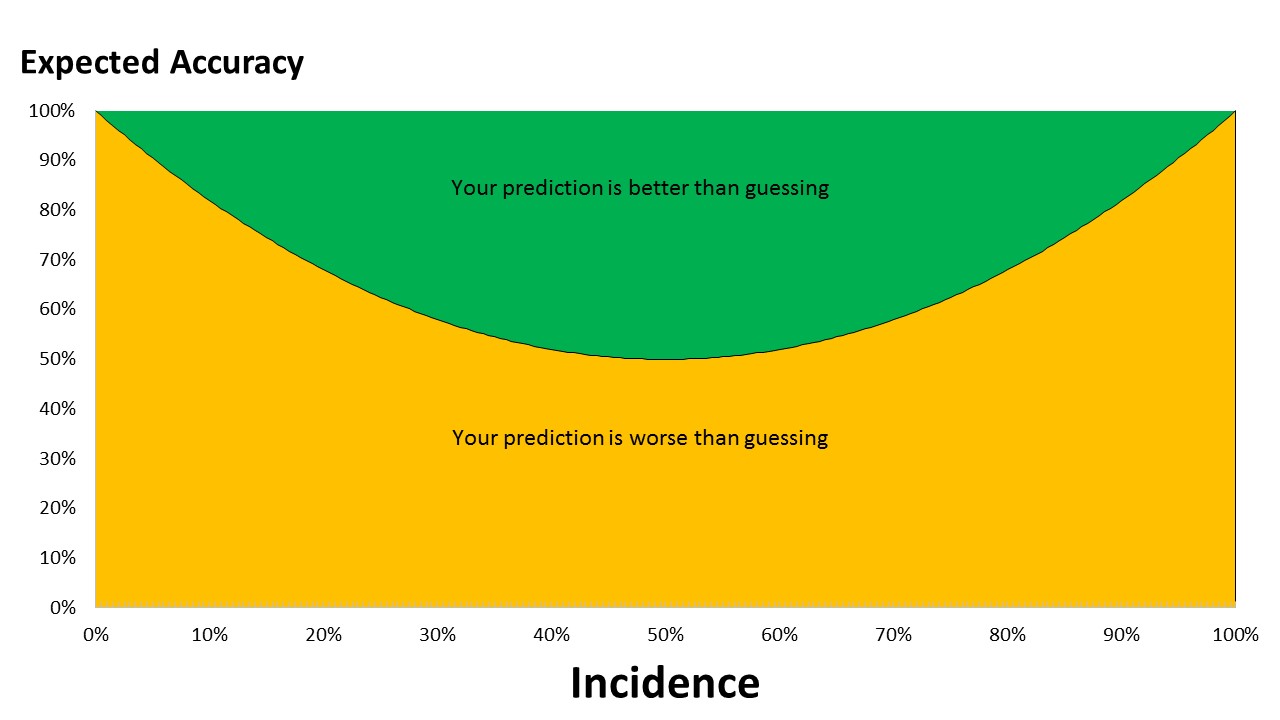
We have been thinking a lot about the relationship between the incidence of the feature we are trying to predict and the usefulness of analytics algorithms. In previous posts (here and here) we looked at the guessing the feature rather than using an analytics model. When the incidence of the feature you are trying to predict is low, it is sometimes worth guessing than running an analytics algorithm since the accuracy will be higher for low incidence features.

If you then consider how Random Forests work (create a family of decision trees at random ->  use the modal value predicted by the family as the correctly classified answer), it becomes clear that these are just a mechanism for creating lots of guesses and when the incidence is low, a guess is better than an analytical prediction. Obviously, this isn't to undermine Random Forests, more an observation as to perhaps why they work so well.

We have never really looked at the efficiency of the KL algorithm vs a straight guess as we work down further into a decision tree. However,  what we have incorporated is a means of more efficient deployment of resources (servers and processors).  The latest release of the product allows users to set a stopping criteria based on the incidence of the predicted feature for a particular branch in the learning tree. As we have seen (here) , incidence levels effect the point at which the user is better off making a guess than relying on an analytics algorithm. The stopping criteria prevents the application going past the point at which a guess would be better.

 

Posted on

Simple Accuracy Calculator

I used the accuracy calculation equation to make this simple form that works out how well a prediction must perform to be better than a weighted guess. For example if the incidence of what we are trying to predict is 40% (gender=female, for example) then the model prediction must have an accuracy greater than 52% for it to be better than randomly assigning 40% of cases to gender is female  and assigning the other 60% to gender isn't female. As this weighted-guess will have an accuracy of 52% over a large sample.

Posted on

Knowing When to Guess

When it comes to designing and implementing algorithms for Knowledge Leaps I have spent a lot of time thinking about accuracy in relation to making predictions. I soon realized that there is a mathematical relationship between the accuracy of a guess and the incidence of what you are trying to predict.

For instance, if you have built a model for predicting whether or not a roulette ball will fall into the zero slot on a roulette wheel with 37 numbers (0-36) then your model has to be correct (at predicting success or failure) at least 94.67% of the time.  However, if you want to predict red or black then your model needs to be correct 50.04% of the time to be better than a pure guess.

The graph below shows the relationship as a function of incidence (the rate of what we are trying to predict).

Broad conclusions we can draw from this relationship:

  • When we are trying to predict outcomes which have an incidence of between 20% and 80%, there is a lot of potential for producing a worthwhile model that can improve on a guess.
  • When the incidence of outcomes is less than 5% and greater than 95%, models need to be delivering 91%+ accuracy to be of any help. This is the realm of medical diagnosis, an area where guesswork isn't welcome.
  • Since 66% of the chart is territory where a guess is better than a model, if we produced random models to make a prediction, 66% of the time a guess would be better. Obviously, if we aggregate up the results of lots of random guesses we can produce more accurate predictions (e.g. Random Forests). However we then run into the issue of not creating human readable models.